Clustering
비지도 군집분석 중 MeanShift와 DBSCAN에 대해 정리하고자 합니다.
MeanShift는 특이한 형태를 지니는 data를 클러스터링 하기에는 한계가 존재하여 이러한 경우 DBSCAN을 사용하는 것으로 알고 있습니다. 해당 코드는 Sklearn 공홈을 참고하였으며 알고리즘의 공식 같은 경우에는 V-Measure: A conditional entropy-based external cluster evaluation measure 논문을 참고하였습니다.
Mean-Shift 클러스터링
- KDE를 이용하여 개별 데이터 포인트들이 데이터 분포가 높은 곳으로 이동하면서 군집화를 수행하는 모델
- 사전에 군집화 개수를 지정하지 않으며 데이터 분포도에 기반해 자동으로 군집화 개수를 정하게 됨
- 비모수 방법론 모델
장점
- 클러스터 개수 정의 불필요
- 이상치의 영향력이 크지 않음
단점
- 알고리즘의 수행시간이 오래 걸림
- 특이한 형태를 지니는 data를 클러스터링 하기에는 한계
파라미터
- Bandwith(대역폭) , quantile(일정 비율 샘플링)
평가지표
- silhouette_score
클러스터링 과정


코드
import numpy as np
from sklearn.cluster import MeanShift, estimate_bandwidth
from sklearn.datasets import make_blobs
# #############################################################################
# 샘플 데이터 생성
centers = [[1, 1], [-1, -1], [1, -1]]
X, _ = make_blobs(n_samples=10000, centers=centers, cluster_std=0.6)
# #############################################################################
# MeanShift를 사용한 컴퓨팅 클러스터링
# 다음 대역폭은 다음을 사용하여 자동으로 감지 할 수 있습니다.
bandwidth = estimate_bandwidth(X, quantile=0.2, n_samples=500)
ms = MeanShift(bandwidth=bandwidth, bin_seeding=True)
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
labels_unique = np.unique(labels)
n_clusters_ = len(labels_unique)
print("number of estimated clusters : %d" % n_clusters_)
# #############################################################################
# 플롯 결과
import matplotlib.pyplot as plt
from itertools import cycle
plt.figure(1)
plt.clf()
colors = cycle('bgrcmykbgrcmykbgrcmykbgrcmyk')
for k, col in zip(range(n_clusters_), colors):
my_members = labels == k
cluster_center = cluster_centers[k]
plt.plot(X[my_members, 0], X[my_members, 1], col + '.')
plt.plot(cluster_center[0], cluster_center[1], 'o', markerfacecolor=col,
markeredgecolor='k', markersize=14)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()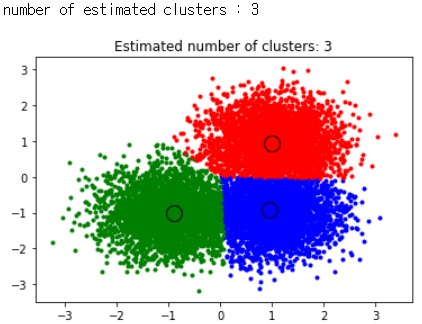
DBSCAN 클러스터링
- 비계층적 군집분석 미리 군집의 개수(K)를 입력해주지 않아도 됨
- 데이터의 밀도를 활용해서 클러스터링
- 가정: 동일한 클래스에 속하는 데이터는 서로 근접하게 분포할 것이다
장점
- 클러스터 개수 정의 불필요하며 알고리즘이 자동으로 클러스터의 수를 찾음
- 잡음 / 이상치에도 견고하며 계산 복잡도도 적음
단점
- 차원의 저주로 인한 역효과
- 데이터를 사용하는 순서에 따라 클러스터링 차이
파라미터
- eps(이웃반경), min_samples(최소 지점의 수), metric(거리 측정 방식)
평가지표
- silhouette_score, ARI, Homogeneity, Completness, V-measure
클러스터링 과정
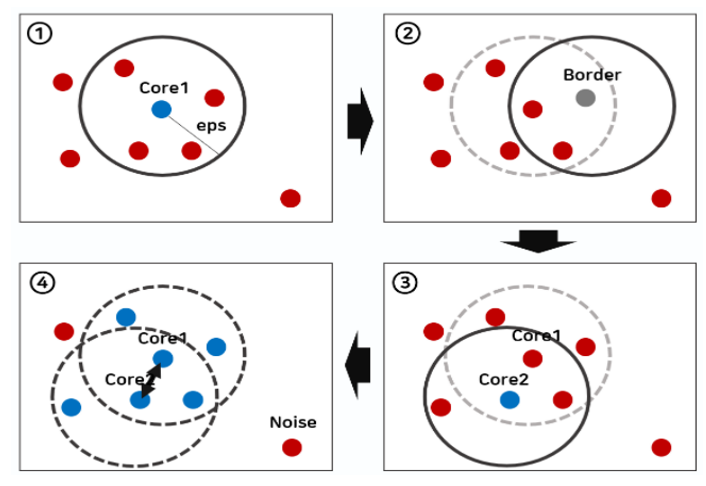

코드
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets import make_blobs
from sklearn.preprocessing import StandardScaler
# #############################################################################
# 샘플 데이터 생성
centers = [[1, 1], [-1, -1], [1, -1]]
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,
random_state=0)
X = StandardScaler().fit_transform(X)
# #############################################################################
# DBSCAN 계산
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
# 레이블의 클러스터 수, 존재하는 경우 노이즈 무시.
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
n_noise_ = list(labels).count(-1)
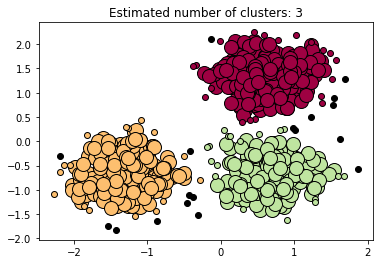
print('Estimated number of clusters: %d' % n_clusters_)
print('Estimated number of noise points: %d' % n_noise_)
print("Homogeneity: %0.3f" % metrics.homogeneity_score(labels_true, labels))
print("Completeness: %0.3f" % metrics.completeness_score(labels_true, labels))
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels))
print("Adjusted Rand Index: %0.3f"
% metrics.adjusted_rand_score(labels_true, labels))
print("Adjusted Mutual Information: %0.3f"
% metrics.adjusted_mutual_info_score(labels_true, labels))
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, labels))
# #############################################################################
# 플롯 결과
import matplotlib.pyplot as plt
# 검정색이 제거되고 대신 노이즈에 사용됩니다.
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
if k == -1:
# 노이즈에 검정색 사용.
col = [0, 0, 0, 1]
class_member_mask = (labels == k)
xy = X[class_member_mask & core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=14)
xy = X[class_member_mask & ~core_samples_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
평가지표
평가지표의 경우 군집의 실제값이 있는 목적 변수가 있을 때 성능을 평가하는 Homogeneity, Completeness, V-measure 그렇지 않을 경우에는 Silhouette coeffcient를 사용하게 됩니다. 또한 표본의 크기와 군집의 수에 따라서 ARI를 사용하게 됩니다.
Homogeneity
- 군집의 실제값이 있는 목적 변수가 있을때 성능 평가
- 각 클러스터의 모든 객체들이 동일한 클래스로부터 온 객체들 일 때, 클러스터링 결과는 동질성을 만족시킴
- 동질성(homogeneity)은 각 유전자의 발현 profile과 유전자가 속하는 군집의 중심 사이의 평균 거리를 계산하는 것
- 0.0에서 1.0까지의 분포를 나타내며 값이 클 수록 좋음

코드
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.homogeneity_score(labels_true, labels_pred)
# 0.66...Completeness
- 군집의 실제값이 있는 목적 변수가 있을때 성능 평가
- 각 클래스의 모든 객체들이 동일한 클러스터의 멤버가 될 때, 클러스터링 결과는 완전성을 만족시킴
- 주어진 범주의 모든 데이터 점이 같은 군집 내에 있는 것을 나타냄
- 척도 값이 클수록 좋은 군집 알고리즘으로 평가

코드
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.completeness_score(labels_true, labels_pred)
#0.42...V-measure
- 군집의 실제값이 있는 목적변수가 있을 때 성능 평가
- Homogeneity와 Completeness의 조화 평균
- 균질성 및 완전성 기준이 얼마나 성공적으로 충족되었는지 명시적으로 측정하는 엔트로피 기반 측정
- 0.0과 1.0사이의 양수 값을 가지며 클수록 좋음
- 표본 수가 1,000개 이상이고 군집화 수가 10개 미만인 경우에는 무작위 표시와 관련화여 정규화 안 되는 문제를 무시(표본의 크기가 작거나 군집 수가 많은 경우 ARI)
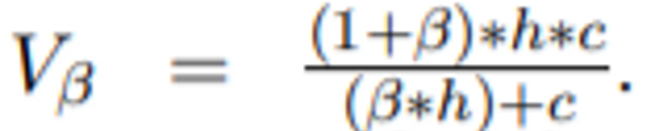
코드
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.v_measure_score(labels_true, labels_pred)
# 0.51...ARI
- Adjusted rand index
- 타깃값으로 클러스터링 평가
- 1(최적일 때)과 0(무작위로 분류될 때) 사이의 값을 제공
- 표본의 크기가 작거나 군집 수가 많은 경우 사용
- Adjusted Rand Index는 성능이 완벽한 경우 1이 됨
- 가장 나쁜 경우로서 무작위 군집화를 하면 0에 가까운 값이 나옴
- 경우에 따라서는 음수가 나옴

코드
from sklearn import metrics
labels_true = [0, 0, 0, 1, 1, 1]
labels_pred = [0, 0, 1, 1, 2, 2]
metrics.adjusted_rand_score(labels_true, labels_pred)
#0.24...Silhouette coefficient
- 타깃값이 필요 없는 군집용 지표(군집의 실제값이 있는 목적 변수가 없을 때 성능 평가)
- 1(최적일 때)과 0(무작위로 분류될때) 사이의 값을 제공
- 각 군집 간의 거리가 얼마나 효율적으로 분리되어 있는지를 나타냄
- 해당 데이터가 같은 군집 내의 데이터와 얼마나 가깝게 군집화 되어있고, 다른 군집에 있는 데이터와는 얼마나 멀리 분리되어 있는지 나태 내는 지표
- 1에 가까운 값 : 근처의 군집과의 거리가 멀다는 의미
- 0에 가까운 값 : 근처의 군집과의 거리가 가깝다는 으미ㅣ
- -(음수)인 값 : 원래 A라는 군집 내의 데이터인데 다른 B 군집에 할당됐다는 의미

코드
from sklearn import metrics
from sklearn.metrics import pairwise_distances
from sklearn import datasets
X, y = datasets.load_iris(return_X_y=True)
import numpy as np
from sklearn.cluster import KMeans
kmeans_model = KMeans(n_clusters=3, random_state=1).fit(X)
labels = kmeans_model.labels_
metrics.silhouette_score(X, labels, metric='euclidean')
# 0.55'Data Analysis' 카테고리의 다른 글
| [시계열] Box-Jenkins 방법을 이용한 ARIMA모형 (0) | 2020.06.17 |
|---|---|
| [크롤링]BeautifulSoup + selenium을 이용한 표 크롤링 (0) | 2020.06.17 |
| [크롤링]BeautifulSoup을 이용한 표 크롤링 (5) | 2020.06.17 |
| [크롤링 오류]This version of ChromeDriver only supports Chrome version (1) | 2020.06.16 |
| [시계열] 홀트의 선형지수평활법, Holt-winter의 계절지수평활법 (0) | 2020.04.22 |